Sensitivity Analysis

The sensitivity analysis layer enables the extraction of local and global sensitivities, which are provided by the LocalSensitivity and GlobalSensitivity classes respectively. The sensitivity is calculated for each performance attribute with respect to all design parameters, resulting in the sensitivity matrix \(\mathbf{S} \in \mathbb{R}^{d_y \times d_x}\), where each entry \(S_{ij}\) represents the sensitivity of the \(i\)-th output to the \(j\)-th input. Due to the fact that both continuous and discrete variables are supported as model inputs, two different cases are distinguished.

For continuous input variables, the sensitivity is quantified using partial derivatives:

\[S_{ij} = \left.\frac{\partial \hat{y}_i(\mathbf{x})}{\partial x_j}\right|_{\mathbf{x} = \mathbf{x^*}}\]

These derivatives are computed through automatic differentiation.

For discrete or categorical inputs, the sensitivity is calculated as the difference between the outputs at the reference design points and the perturbed points:

\[S_{ij} = \hat{y}_i(\mathbf{x^*}) - \hat{y}_i(\mathbf{x'})\]

Here, \(\mathbf{x^*}\) is the reference design point, and \(\mathbf{x'}\) is the perturbed point where the \(j\)-th entry of \(\mathbf{x^*}\) has been switched to an alternative category.

Local Sensitivity Analysis

The LocalSensitivity analysis examines the impact of small perturbations in design parameters \(\mathbf{x}\) on the performance space \(\hat{\mathbf{y}}\), evaluated at a reference point \(\mathbf{x^*}\) in the design space.

Local sensitivity analysis helps in:

  • Understanding the behavior in the immediate neighborhood of a design point.

  • Helps to identify design parameters that have a strong influence on the performance attributes.

  • Guides the direction of parameter changes aimed at achieving a target performance

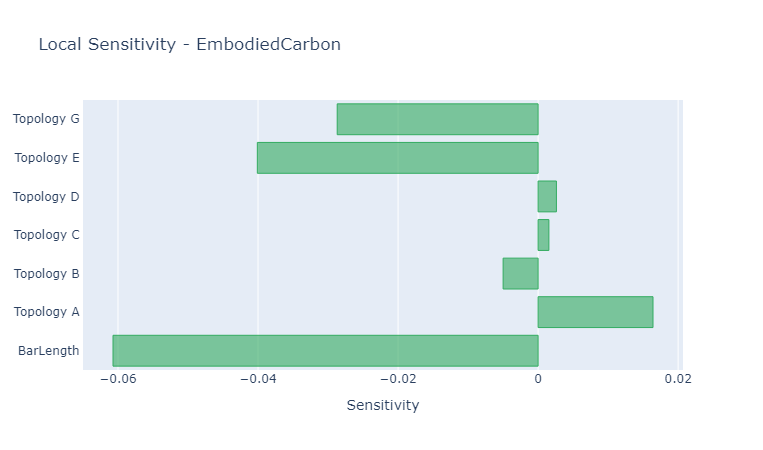
The image cannot be displayed.

Fig. 1: Local embodied carbon sensitivity of a grid shell design with respect to its design parameters.

Global Sensitivity Analysis

The GlobalSensitivity analysis class extends the sensitivity analysis to multiple design points. Instead of evaluating a single reference point, it computes sensitivities for any set of design points.

Global sensitivity analysis helps in:

  • Assessing how parameter sensitivities change across different regions of the design space.

  • Identifying globally influential parameters, not just at a specific point.

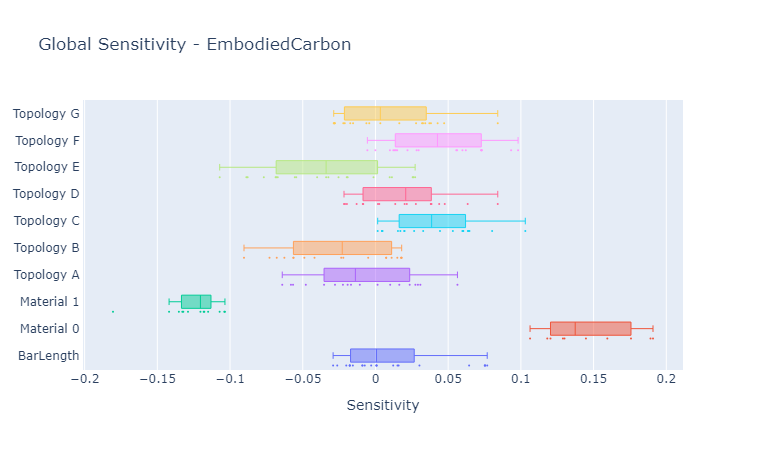
The image cannot be displayed.

Fig. 2: Global embodied carbon sensitivities of the grid shell design space with respect to its design parameters.

Hint

Due to the approximation inherent in the trained model, the local sensitivity analysis may produce noisy results. To obtain more reliable local sensitivity estimates, consider sampling multiple nearby points around the location of interest and analyzing their sensitivities using the GlobalSensitivity functionality.